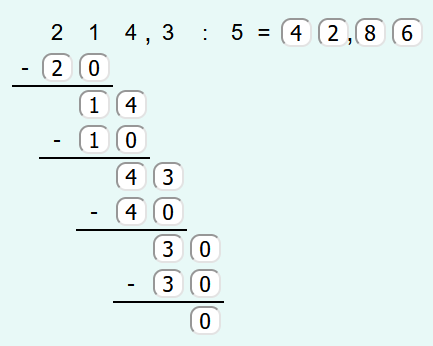Über den Rechner
Dieser Online-Rechner kann auf 2 Arten verwendet werden:
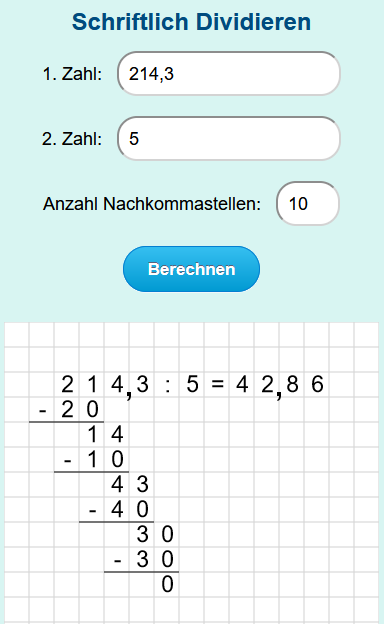
- Ergebnis anzeigen: Mit diesem Online-Rechner lässt sich eine Zahl durch eine andere dividieren (teilen). Das Ergebnis der Rechnung wird samt Rechenweg und Übertrag angezeigt.
- selber rechnen: Dieser Rechner kann genutzt werden, um das schriftliche Dividieren zu üben. Man füllt selber die Felder für die Lösung und den Lösungsweg aus und kann sich danach anzeigen lassen, ob man richtig gerechnet hat.
Es lässt sich auswählen, ob die Division mit Rest oder mit Komma ausgeführt werden soll. Wenn "mit Rest" ausgewählt ist, müssen beide Zahlen ganze Zahlen sein. Bei der Berechnung mit Komma dürfen die Zahlen auch Kommazahlen sein. In beiden Fällen müssen die Zahlen positiv sein.
Wie funktioniert die schriftliche Division?
Als erstes Beispiel soll die Zahl 1392 durch 6 geteilt werden.
Jetzt sieht man sich an, wie häufig die 6 in die erste Ziffer der ersten Zahl passt. 6 passt 0 mal in die 1. Also sieht man sich an, wie häufig die 6 in die ersten beiden Ziffern, also die 13, passt. Das sind 2 mal, weil 2 * 6 = 12. Wenn man nicht sicher ist, ob die 6 nicht vielleicht auch 3 mal in die 13 passen würde, könnte man 6 * 3 berechnen. Das sind 18 (was größer als 13 ist) und somit passt die 6 nicht 3 mal in die 13. Jetzt schreibt man die Zahl, wie häufig die 6 in die 13 passt (also 2), in die Lösung und das Ergebnis aus 6 * 2 (also 12) unter die 13.
Als nächstes wird die obere Zahl von der unteren abgezogen. Man berechnet also 13 - 12.
Neben diese Zahl schreibt man die nächste Ziffer der ersten Zahl. Das ist in diesem Fall die 9.
Jetzt ermittelt man wie häufig die 6 in die 19 passt. Das tut sie 3 mal, weil 6 * 3 = 18 (kleiner als 19) und 6 * 4 = 24 (größer als 19) gilt. Also schreibt man wieder die 3 in die Lösung und die 18 unter die 19.
Danach führt man wieder die Subtraktion durch und schreibt die nächste Ziffer der ersten Zahl daneben.
Nun sieht man sich wieder an, wie häufig die 6 in die 12 passt und das sind genau 2 mal. Also schreibt man die 2 in die Lösung und die 12 unter die 12.
Und ein weiteres mal zieht man die untere Zahl von der oberen ab.
Bei der ersten Zahl sind keine Ziffern mehr übrig und da die Subtraktion 0 ergeben hat, ist man fertig. Das Ergebnis ist 232.
Aber wie wird damit umgegangen, wenn alle Ziffern der ersten Zahl aufgebraucht sind, aber im Rechenweg keine 0 herausgekommen ist?
In dem Fall hat man die Möglichkeit entweder das Ergebnis mit Rest oder mit Komma anzugeben.
schriftliche Division mit Rest
Bei der schriftlichen Division mit Rest wird in diesem Fall hinter die Lösung noch ein "R" gefolgt von der letzten Zahl im Rechenweg geschrieben.
schriftliche Division mit Komma
Als Beispiel soll 1395 durch 6 dividiert werden. Zuerst rechnet man wie oben beschrieben bis zu der Stelle, wo von der ersten Zahl keine Ziffern mehr übrig sind.
Hat man diese Stelle erreicht, wird an die Lösung ein Komma angehängt.
Anstatt von Ziffern aus der ersten Zahl hängt man nun eine 0 an die unterste Zahl im Rechenweg an.
Jetzt macht man wieder genau das Gleiche, was man in den vorherigen Schritten auch gemacht hat. Man berechnet, wie häufig die 6 in die 30 passt. Also 5 mal.
Und führt dann wieder die Subtraktion durch.
Das macht man so lange, bis die Lösung der Subtraktion eine 0 ist. Das ist in diesem Fall der Fall und somit ist 232,5 das Ergebnis.
schriftliche Division mit Komma und Periode
In diesem Abschnitt soll 17 durch 11 geteilt werden. Möchte man die Berechnung durchführen, erhält man nach wenigen Schritten:
Sieht man sich den Rechenweg an, dann kam etwas weiter oben schon einmal eine 6 heraus und an diese 6 wurde eine 0 angehängt, weil alle Ziffern von Zahl 1 aufgebraucht waren.
Man war also schonmal in der Situation, in der man sich jetzt wieder befindet. Wenn man nun weiter rechnet, werden immer und immer wieder die gleichen Zahlen heraus kommen. Die Lösung würde unendlich lang werden und wie folgt aussehen:
1,5454545454545454545454545454....
Für diesen Fall gibt es einen sogenannten Periodenstrich. Er zeigt an, dass die Zahlenfolge, die unter diesem Strich steht, sich unendlich lange wiederholt. Der Periodenstrich beginnt ab der Ziffer in der Lösung, ab der sich die dazugehörige Zahl im Lösungsweg wiederholt.
Komma in der ersten Zahl
Wenn die erste Zahl ein Komma enthält, wird in dem Moment, in dem die erste Nachkomma-Ziffer an eine Ziffer im Rechenweg gehängt wird, in der Lösung ein Komma angehängt.
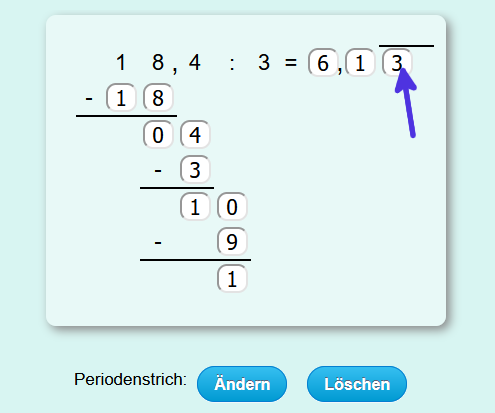
Als Beispiel soll 64,34 durch 2 geteilt werden.
Komma in der zweiten Zahl
Wenn die zweite Zahl ein Komma enthält, werden beide Zahlen so lange mit 10 multipliziert, bis die zweite Zahl kein Komma mehr enthält.
Hinweise zum Rechner
Im Eingabefeld "Anzahl Nachkommastellen" kann festgelegt werden wie viele Nachkommastellen das Ergebnis maximal haben soll. Der Rest wird einfach abgeschnitten/abgerundet.
Wenn bei Erreichen der festgelegten Anzahl an Nachkommastellen noch Ziffern der ersten Zahl übrig sind, wird trotzdem weiter gerechnet, bis die Ziffern alle aufgebraucht sind. Somit kann das Ergebnis mehr Nachkommastellen haben als vorher festgelegt wurde.
Variante "Ergebnis anzeigen":
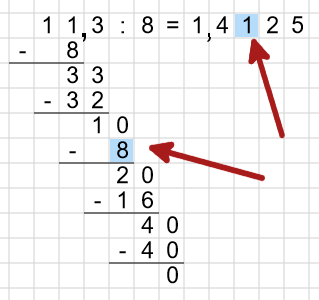
Wenn sich der Mauszeiger über einer Ziffer der Lösung befindet, wird die dazugehörige Zeile im Rechenweg markiert.
Wenn sich der Mauszeiger über dem Periodenstrich vom Ergebnis befindet, wird die Zeile im Lösungsweg markiert, ab der sich die Zwischenergebnisse wiederholen.
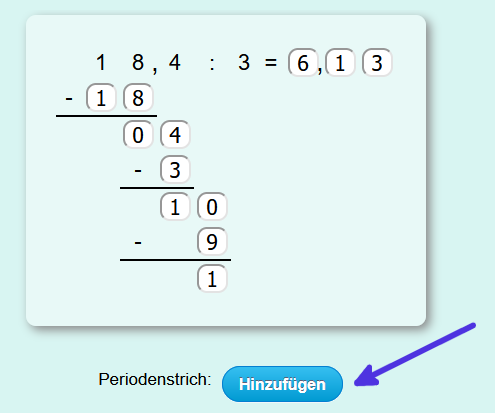
Variante "selber rechnen":
Um einen Periodenstrich zu setzen muss zuerst auf "Periodenstrich: Hinzufügen" geklickt werden und dann auf das Feld der Lösung, ab dem der Periodenstrich beginnen soll.